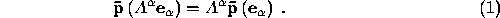
Let the components of 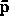 be
be 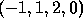 , those of
, those of
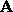 be
be 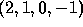 and those of
and those of 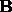 be
be
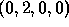 . Find (i)
. Find (i) 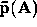 ; (ii)
; (ii)
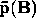 ; (iii)
; (iii)
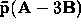 ; (iv)
; (iv)
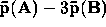 .
.
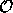 :
:
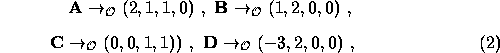
(2a) show that they are linearly independent.
(2b) Find the components of 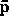 if
if
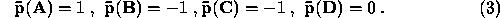
(2c) Find the value of 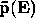 for
for
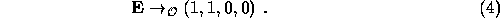
(2d) Determine whether the one- forms 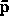 ,
, 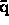 ,
,
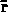 and
and 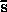 are linearly independent if
are linearly independent if
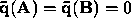 ,
,
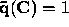 ,
, 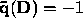 ,
,
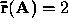 ,
,
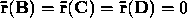 ,
, 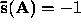 ,
,
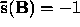 ,
, 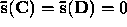 .
.
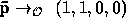 and
and
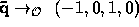 be two one forms. Prove by
trying two vectors
be two one forms. Prove by
trying two vectors 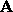 and
and 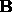 as arguments, that
as arguments, that
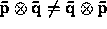 .
Then find the components of
.
Then find the components of 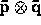 .
.
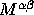 as the matrix
as the matrix
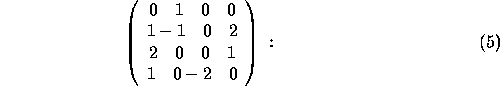
find (i) the components of the symmetric tensor 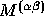 and the antisymmetric tensor
and the antisymmetric tensor 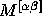 ; (ii) the components
of
; (ii) the components
of 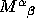 ; (iii) the components of
; (iii) the components of
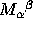 ; and (iv) the components of
; and (iv) the components of 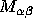 .
.
(4b) For the tensor whose components are 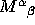 , does it
make sense to speak of its symmetric and antisymmetric parts? If so,
define them. If not, say why.
, does it
make sense to speak of its symmetric and antisymmetric parts? If so,
define them. If not, say why.
(4c) Raise an index of the metric tensor to prove that
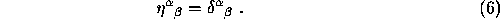
 tensor, B is a symmetric
tensor, B is a symmetric 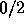 tensor, C is an arbitrary
tensor, C is an arbitrary 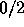 tensor, and D is an arbitrary
tensor, and D is an arbitrary
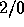 tensor. Prove:
tensor. Prove:
(5a) 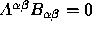 ;
;
(5b) 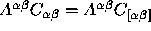 ;
;
(5c) 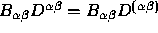 .
.
 , the four- vector fields
, the four- vector fields 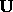 and
and
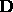 have the components [ with units where c=1 ]:
have the components [ with units where c=1 ]:
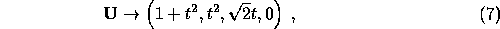
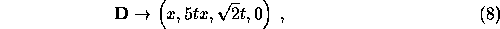
and the scalar 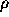 has the value
has the value
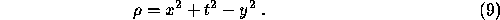
(6a) Find  ,
,  ,
,
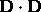 . Is
. Is 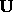 suitable as a 4-
velocity field? Is
suitable as a 4-
velocity field? Is 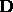 ?
?
(6b) Find the spatial velocity 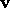 of a particle whose
four- velocity is
of a particle whose
four- velocity is 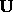 , for arbitrary t. What happens to
it in the limits
, for arbitrary t. What happens to
it in the limits 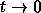 ,
, 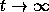 ?
?
(6c) Find 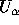 for all
for all 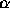 .
.
(6d) Find 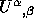 for all
for all 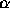 and
and 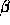 .
.
(6e) Show that 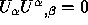 for all
for all 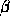 .
Show that
.
Show that 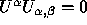 for all
for all 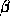 .
.
(6f) Find 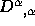 .
.
(6g) Find 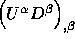 for all
for all 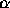 .
.
(6h) Find 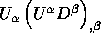 and
compare with (f) above. Why are the two answers similar?
and
compare with (f) above. Why are the two answers similar?
(6i) Find 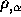 for all
for all 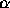 . Find
. Find 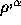 for
all
for
all 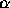 . What are the numbers
. What are the numbers 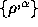 the
components of?
the
components of?
(6j) Find 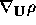 ,
,
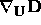 .
. 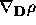 and
and 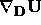 .
.